Glosario

Ten en cuenta algunos breves significados: 

1. Punto: Es uno de los entes fundamentales, junto con la recta y el plano. Es considerado concepto primario, es decir, que sólo es posible describirlo en relación con otros elementos similares. Se suele describir apoyándose en los postulados característicos, que determinan las relaciones entre los entes geométricos fundamentales.

2. Segmento: Es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales. Los puntos A y B son extremos del segmento y los puntos sobre la recta a la que pertenece el segmento (la «recta sostén»), serán interiores o exteriores al segmento según pertenezcan o no a este.

3. Recta: Una recta es una sucesión infinita de puntos, situados en una misma dirección. Tiene una sola dimensión: la longitud. Las rectas se nombran mediante dos de sus puntos o por una letra minúscula. Una recta indica una dirección y dos sentidos contrarios.

Dos puntos determinan una recta.

4.Semirrecta: Identifica a cada uno de los fragmentos en que toda recta puede ser dividida por cualquiera de los puntos que la componen. 


5. Plano: Un plano es objeto ideal que solo posee dos dimensiones, y contiene infinitos puntos y rectas.Cuando se habla de un plano, se está hablando del objeto geométrico que no posee volumen, es decir bidimensional, y que posee un número infinito de rectas y puntos.

6. Semiplano: Un semiplano es cada una de las partes en que queda dividido un plano por una cualquiera de sus rectas.

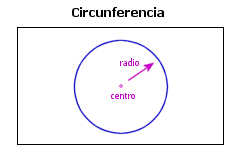
7.Un círculo: Es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida. 

8. La circunferencia: Es un contorno contínuamente curvado, cuyos puntos están todos a la misma distancia de un punto central, llamado centro del círculo. La distancia constante de cualquier punto de la circunferencia se denomina radio. 

9. Un triángulo:  Es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos(que no se encuentran alineados, es decir: no colinelaes . Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 ángulos exteriores, 3 lados y 3 vértices. 

10. El cuadrado: Es la figura geométrica formada por cuatro líneas rectas de igual longitud, denominadas lados, que forman ángulos perfectamente rectos en los puntos de unión entre ellas (esquinas a 90º). 
         

Añadir leyenda

 11. Rectángulo: Es un paralelogramo cuyos cuatro lados forman ángulos rectosentre sí. Los lados opuestos tienen la misma longitud. El perímetro de un rectángulo es igual a la suma de todos sus lados.

El área de un rectángulo es igual al producto de dos de sus lados contiguos.

12. El rombo: Es un polígono que tiene los cuatro lados iguales y los ángulos son iguales dos a dos. 

( Dos ángulos son agudos y los otros dos obtusos) Para hallar el área se utiliza la formula siguiente:

 A = (D · d) / 2

(Es decir, el área es igual al producto de la diagonal mayor (D) por la diagonal menor (d) y el resultado se divide entre dos)

13. trapecio: Es un cuadrilátero que tiene dos lados paralelos y otros dos que no lo son. Los lados paralelos se llaman bases del trapecio y la distancia entre ellos altura. Se denomina mediana al segmento que tiene por extremos los puntos medios de los lados no paralelos. Un cuadrilátero sin lados paralelos recibe el nombre de trapezoide.

14. Un paralelogramo: Es un tipo especial de cuadrilátero (un polígono formado por cuatro lados) cuyos lados son paralelos dos a dos.

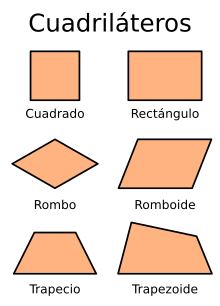
15. Un cuadrilátero: Es un polígono que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre da como resultado 360º.