Encuentra los aspectos mas básicos de la trigonometria!!

Definición:

La palabra trigonometria se origina en Grecia dividida en  las palabras “ trígono” que quiere decir triángulo y “metron” que es medida. En otras palabras literalmente quiere decir “medir triángulos” . Interviene en diversas áreas de las matemáticas en las que se necesita trabajar con precisión. La trigonometria  cuenta con una amplia variedad de aplicaciones.

La trigonometria estudia: 

• Estudia  las medidas de los lados de triángulos rectángulos, lo que hoy llamamos “teorema de Pitágoras” porque son tres números enteros que cumplen el teorema de Pitágoras 

• Estudia las razones trigonométricas: seno, coseno; tangente,cotangente; secante y cosecante.

• Se encarga de calcular los elementos de los triángulos. Para esto se dedica a estudiar las relaciones entre los ángulos y los lados de los triángulos.Existen tres unidades que emplea la trigonometria para la medición de ángulos: el radián (considerada como la unidad natural de los ángulos, establece que una circunferencia completa puede dividirse en 2 pi radianes), el gradián o grado centesimal (que permite dividir la circunferencia en cuatrocientos grados centesimales) y el grado sexagesimal (se usa para dividir la circunferencia en trescientos sesenta grados sexagesimales). 

• Realiza la  identidad trigonométrica, esta se encarga de  la igualdad que involucra a funciones trigonométricas y que resultan verificables para cualquier valor de las variables (los ángulos sobre los que se aplican las funciones).

• La trigonometria se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

• Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.  

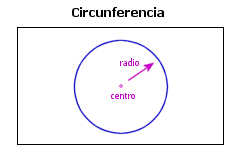
• La trigonometria tiene una razón trigonométrica llamada circunferencia goniométrica que se caracteriza por el hecho de que su radio es la unidad en sí y su centro no es otro que el origen de las coordenadas pertinentes. Todo ello sin olvidar tampoco que en la misma los ejes de las coordenadas lo que hacen es delimitar cuatro cuadrantes que están enumerados en lo que es el sentido contrario al que marcan las agujas de un reloj.

• La llamada trigonometria esférica es aquella parte de las Matemáticas que se centra en proceder al estudio de lo que son los triángulos de tipo esférico.

• Trigonometria plana. En este caso, como su propio nombre indica, es aquella ciencia que tiene como objeto el análisis y estudio de los diversos triángulos planos.

Reseña histórica de la trigonometria:

Tablilla babilonia Plimpton 322.

Los antiguos egipcios y los babilonios conocían ya los teoremas sobre las proporciones de los lados de los triángulos semejantes. Pero las sociedades pre-helénica carecían de la noción de una medida del ángulo y por lo tanto, los lados de los triángulos se estudiaron en su medida, un campo que se podría llamar trilaterometría.

Los astrónomos babilonios llevaron registros detallados sobre la salida y puesta de las estrellas, el movimiento de los planetas y los eclipses solares y lunares, todo lo cual requiere la familiaridad con la distancia angular medida sobre la esfera celeste. Sobre la base de una interpretación de la tablilla cuneiforme Plimpton 322 (c. 1900 aC), algunos incluso han afirmado que los antiguos babilonios tenían una tabla de secantes. Hoy, sin embargo, hay un gran debate acerca de si se trata de una tabla de ternas pitagóricas, una tabla de soluciones de ecuaciones segundo grado, o una tabla trigonométrica.

Papiro de Ahmes

Los egipcios, en el segundo milenio antes de Cristo, utilizaban una forma primitiva de la trigonometría, para la construcción de las pirámides. El Papiro de Ahmes, escrito por el escriba egipcio Ahmes (c. 1680-1620 aC), contiene el siguiente problema relacionado con la trigonometría:

"Si una pirámide es de 250 codos de alto y el lado de su base es de 360 codos de largo, ¿cuál es su Seked?

La solución, al problema, es la relación entre la mitad del lado de la base de la pirámide y su altura. En otras palabras, la medida que se encuentra para la seked es la cotangente del ángulo que forman la base de la pirámide y su cara.

La historia de la trigonometría no comienza formalmente hasta el siglo XVI o XVII, cuando comenzó su estudio propiamente tal; hay algo de polémica sobre dos tratados de esas épocas que si bien no usan el nombre como tal sí tratan sobre el tema. Ya para mediados del siglo XIX la trigonometría era estudiada según la conocemos hoy día.

Glosario

Ten en cuenta algunos breves significados: 

1. Punto: Es uno de los entes fundamentales, junto con la recta y el plano. Es considerado concepto primario, es decir, que sólo es posible describirlo en relación con otros elementos similares. Se suele describir apoyándose en los postulados característicos, que determinan las relaciones entre los entes geométricos fundamentales.

2. Segmento: Es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales. Los puntos A y B son extremos del segmento y los puntos sobre la recta a la que pertenece el segmento (la «recta sostén»), serán interiores o exteriores al segmento según pertenezcan o no a este.

3. Recta: Una recta es una sucesión infinita de puntos, situados en una misma dirección. Tiene una sola dimensión: la longitud. Las rectas se nombran mediante dos de sus puntos o por una letra minúscula. Una recta indica una dirección y dos sentidos contrarios.

Dos puntos determinan una recta.

4.Semirrecta: Identifica a cada uno de los fragmentos en que toda recta puede ser dividida por cualquiera de los puntos que la componen. 


5. Plano: Un plano es objeto ideal que solo posee dos dimensiones, y contiene infinitos puntos y rectas.Cuando se habla de un plano, se está hablando del objeto geométrico que no posee volumen, es decir bidimensional, y que posee un número infinito de rectas y puntos.

6. Semiplano: Un semiplano es cada una de las partes en que queda dividido un plano por una cualquiera de sus rectas.

7.Un círculo: Es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida. 

8. La circunferencia: Es un contorno contínuamente curvado, cuyos puntos están todos a la misma distancia de un punto central, llamado centro del círculo. La distancia constante de cualquier punto de la circunferencia se denomina radio. 

9. Un triángulo:  Es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos(que no se encuentran alineados, es decir: no colinelaes . Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 ángulos exteriores, 3 lados y 3 vértices. 

10. El cuadrado: Es la figura geométrica formada por cuatro líneas rectas de igual longitud, denominadas lados, que forman ángulos perfectamente rectos en los puntos de unión entre ellas (esquinas a 90º). 
         

Añadir leyenda

 11. Rectángulo: Es un paralelogramo cuyos cuatro lados forman ángulos rectosentre sí. Los lados opuestos tienen la misma longitud. El perímetro de un rectángulo es igual a la suma de todos sus lados.

El área de un rectángulo es igual al producto de dos de sus lados contiguos.

12. El rombo: Es un polígono que tiene los cuatro lados iguales y los ángulos son iguales dos a dos. 

( Dos ángulos son agudos y los otros dos obtusos) Para hallar el área se utiliza la formula siguiente:

 A = (D · d) / 2

(Es decir, el área es igual al producto de la diagonal mayor (D) por la diagonal menor (d) y el resultado se divide entre dos)

13. trapecio: Es un cuadrilátero que tiene dos lados paralelos y otros dos que no lo son. Los lados paralelos se llaman bases del trapecio y la distancia entre ellos altura. Se denomina mediana al segmento que tiene por extremos los puntos medios de los lados no paralelos. Un cuadrilátero sin lados paralelos recibe el nombre de trapezoide.

14. Un paralelogramo: Es un tipo especial de cuadrilátero (un polígono formado por cuatro lados) cuyos lados son paralelos dos a dos.

15. Un cuadrilátero: Es un polígono que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre da como resultado 360º.

Conoce Junto a Donald el Fantástico Mundo de las Matematicas!!!

Donald en el Mundo de las matemáticas.

Con ayuda de Donald conocerás algunos aspectos simples de la utilidad de las matemáticas. 

Donald como explorador, se introduce en un mundo desconocido, en el cual se siente muy sorprendido ya que durante su camino encuentra nuevos descubrimientos como lo son arboles con las raíces cuadradas, un rió de números  pero en especial un extraño animal con cuerpo de lápiz  el cual este reta a Donald a una partida de tres en raya. Observa luego tres figuras geométricas circulo, rectángulo y triangulo. las cuales al juntarse forman un rostro, el cual empieza a recitar los dígitos del numero pi. Descubriendo así que se trata del mundo de las matemáticas. 

 Después, guiado por el narrador, el pato Donald viaja a la antigua Grecia para conocer a los pitagóricos  los cuales fueron creadores de la escala musical, allí descubre como funcionan las notas musicales. Aprende las proporciones que se encuentran en la estrella de cinco puntas, proporciones las cuales conducen al numero áureo y al rectángulo perfecto. Luego observamos el pentagrama o estrella de cinco puntas, y podemos observar que la proporción áurea se encuentra en muchos lugares de la naturaleza, la cual ha sido empleada por artistas, arquitectos, escultores, pintores, en sus obras mas famosas.

El pato Donald  descubre el empleo de la lógica matemática en el ajedrez, y la presencia de las matemáticas y de la geometría en los juegos y deportes. Así también llega a un famoso, divertido y entretenido juego el billar en su modalidad de carambola a tres bandas, y el narrador le enseña cómo calcular el modo de obtener carambolas sencillas usando las marcas que aparecen en los bordes de la mesa de billar y sumando y restando números y fracciones simples.

Por último el corto nos enseña a utilizar la imaginación, ese poder de nuestra mente mediante el cual podemos ver las figuras geométricas, la esfera, el cono, el paraboloide, el cilindro... que luego tendrán aplicación en la óptica, ingeniería, mecánica, astronomía... Esa misma imaginación nos ayudará a ir abriendo las infinitas puertas del conocimiento que todavía   nos quedan por abrir. 

Obsérvalo con mucha atención y viaja con Donald al maravilloso mundo de las matemáticas!!